Другие дисциплины › Методы исследования › Прогнозирование национальной экономики

Разработка прогноза с помощью метода наименьших квадратов. Пример решения задачи

Экстраполяция - это метод научного исследования, который основан на распространении прошлых и настоящих тенденций, закономерностей, связей на будущее развитие объекта прогнозирования. К методам экстраполяции относятся метод скользящей средней, метод экспоненциального сглаживания, метод наименьших квадратов.

Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии. Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии.

Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Так, если рост выпуска продукции ожидается в арифметической прогрессии, то сглаживание производится по прямой. Если же оказывается, что рост идет в геометрической прогрессии, то сглаживание надо производить по показательной функции.

Рабочая формула метода наименьших квадратов: У t+1 = а*Х + b, где t + 1 – прогнозный период; Уt+1 – прогнозируемый показатель; a и b - коэффициенты; Х - условное обозначение времени.

Расчет коэффициентов a и b осуществляется по следующим формулам:

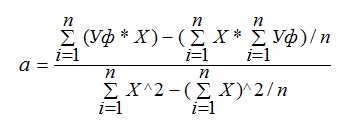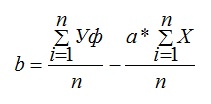где, Уф – фактические значения ряда динамики; n – число уровней временного ряда;

Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной.

Развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Отсюда ясно, что развитие явления во времени выступает как результат действия этих факторов.

Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых сложных задач предпрогнозного анализа.

Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле:

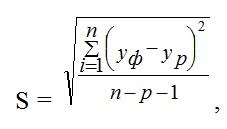где Уф – фактические значения ряда динамики; Ур – расчетные (сглаженные) значения ряда динамики; n – число уровней временного ряда; р – число параметров, определяемых в формулах, описывающих тренд (тенденцию развития).

Недостатки метода наименьших квадратов:

• при попытке описать изучаемое экономическое явление с помощью математического уравнения, прогноз будет точен для небольшого периода времени и уравнение регрессии следует пересчитывать по мере поступления новой информации;
• сложность подбора уравнения регрессии, которая разрешима при использовании типовых компьютерных программ.

Пример применения метода наименьших квадратов для разработки прогноза

Задача. Имеются данные, характеризующие уровень безработицы в регионе, %

• Постройте прогноз уровня безработицы в регионе на ноябрь, декабрь, январь месяцы, используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.
• Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
• Сравните полученные результаты, сделайте выводы.

Решение методом наименьших квадратов

Для решения составим таблицу, в которой будем производить необходимые расчеты:

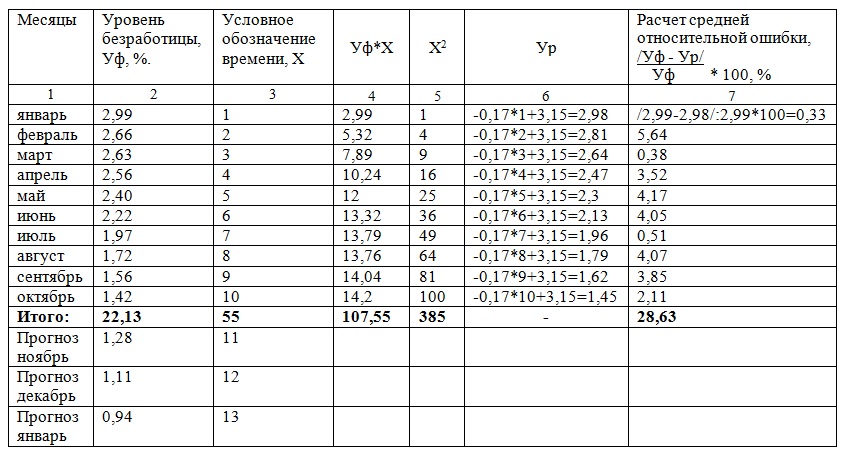Определим условное обозначение времени как последовательную нумерацию периодов базы прогноза (графа 3). Рассчитаем графы 4 и 5. Расчетные значения ряда Ур определим по формуле У t+1 = а*Х + b, где t + 1 – прогнозный период; Уt+1 – прогнозируемый показатель; a и b - коэффициенты; Х - условное обозначение времени.

Коэффициенты a и b определим по следующим формулам:

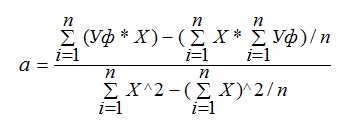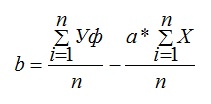где, Уф – фактические значения ряда динамики; n – число уровней временного ряда.
а = [107,55 – (55*22,13)/10] / [385 – 55²/10] = - 0,17
b = 22,13/10 – (-0,17)*55/10 = 3,15

Далее определяем прогнозное значение:
У ноябрь = -0,17*11 + 3,15 = 1,28
У декабрь = -0,17*12 + 3,15 = 1,11
У январь = -0,17*12 + 3,15 = 0,94

Рассчитываем среднюю относительную ошибку по формуле:

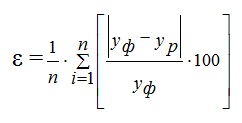ε = 28,63/10 = 2,86% < 10% - точность прогноза высокая.

Вывод: Сравнивая результаты, полученные при расчетах методом скользящей средней, методом экспоненциального сглаживания и методом наименьших квадратов, можно сказать, что средняя относительная ошибка при расчетах методом экспоненциального сглаживания попадает в пределы 20-50%. Это значит, что точность прогноза в данном случае является лишь удовлетворительной.

В первом и третьем случае точность прогноза является высокой, поскольку средняя относительная ошибка менее 10%. Но метод скользящих средних позволил получить более достоверные результаты (прогноз на ноябрь – 1,52%, прогноз на декабрь – 1,53%, прогноз на январь – 1,49%), так как средняя относительная ошибка при использовании этого метода наименьшая – 1,13%.

Другие статьи по данной теме:

• назад: Прогнозирование на основе метода экспоненциального сглаживания. Пример решения задачи
• далее: Прогнозирование сезонных явлений (сезонных колебаний). Пример решения задачи
• Основы корреляционного анализа. Примеры анализа прямолинейной связи при парной корреляции

Список использованных источников

1. Научно-методические рекомендации по вопросам диагностики социальных рисков и прогнозирования вызовов, угроз и социальных последствий. Российский государственный социальный университет. Москва. 2010;
2. Владимирова Л.П. Прогнозирование и планирование в условиях рынка: Учеб. пособие. М.: Издательский Дом «Дашков и Ко», 2001;
3. Новикова Н.В., Поздеева О.Г. Прогнозирование национальной экономики: Учебно-методическое пособие. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2007;
4. Слуцкин Л.Н. Курс МБА по прогнозированию в бизнесе. М.: Альпина Бизнес Букс, 2006.